Hello mathematicians! As a teacher and an individual who loves math, one of my favorite concepts to teach is our base 10 system. Learning the patterns in our base 10 system and applying them to solve math problems is one of the most important things learners do in math. Because it provides the foundation for operations like addition and because it can be difficult to understand, I thought I would write a blog post about our base 10 system.
Throughout history and over the course of many, many, many discussions, mathematicians created a system where each place value within a number was ten times bigger than the place value to the right of it. This is called a base 10 system. To explain this a little more, let’s look at the place values within a number:
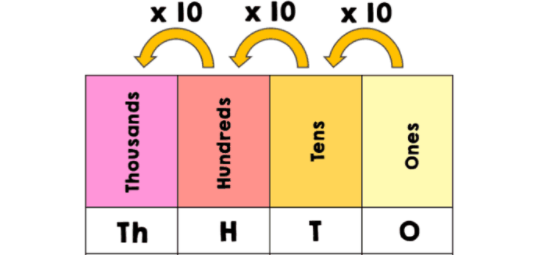
The ones place is the smallest place value within a whole number (decimals will be discussed in another blog post 😊). The tens place, directly to the left of it, is ten times larger than the ones place (think 10 x 1 = 10). The hundreds place, directly left of the tens place, is ten times larger than the tens (think 10 x 10 = 100). The thousands place, directly left of the hundreds place, is ten times larger than the hundreds (think 100 x 10 = 1000). Because this pattern continues forever and because the place value to the left is always ten times bigger than the previous place value, we have a base 10 system!
Now, why is this important? Well, it’s important because this concept directly relates to addition and subtraction. By learning we have a base 10 system, learners begin to understand we can only have 0-9 as digits in each place value. This becomes important when adding and subtracting because if we have a digit that is larger than 9, we must either regroup or ungroup (depending on the operation) to make the digit less than 10.
That’s a lot to take in at once, isn’t it?
Well, let’s look at an example of this together:
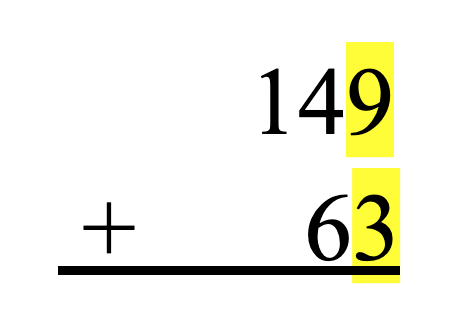
To solve this problem, we first must look in the ones place. We are going to add 9 ones plus 3 ones together. In doing so, we have 12 ones. We can’t write 12 underneath the 3 because 12 is larger than 9, thus breaking our less than 10-digit rule. So, we must take 10 of the 12 ones and trade them in for a ten. 10 ones are the same thing as one ten. We will write a little one above the tens place to represent the new ten we just made. As a result of trading in 10 ones for 1 ten, we now have 2 ones leftover. We will write this 2 in the ones place of our answer. Our problem will now look like this:
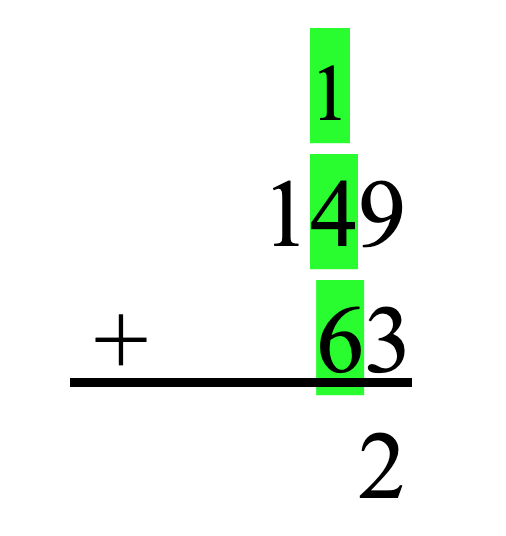
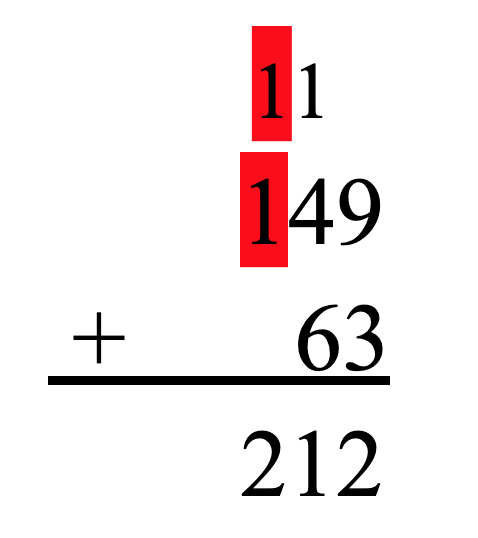
We repeat the same process with our tens place. We add our tens (1 + 4 + 6) to get 11 tens. Once again, 11 breaks our less than 10-digit rule, so we need to make a new hundred. 10 tens is the same thing as one hundred. So, we will write another little one above the hundreds place to represent the new hundred we just made. After making our new hundred with 10 tens, we are left with 1 ten. We will write this 1 in the tens place of our answer. Our problem now looks like this:
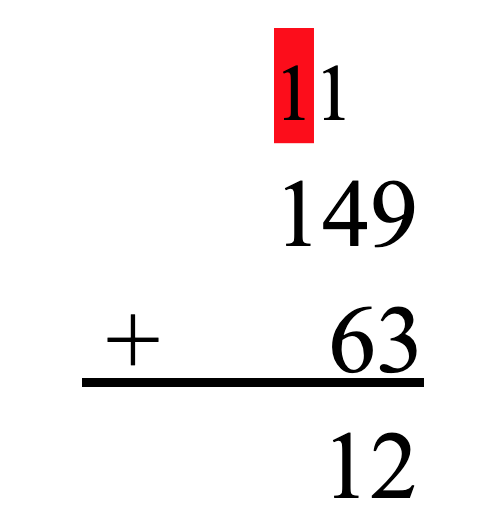
The same steps listed above are applied to the hundreds place to give us a final answer of 212.
That’s a lot of math we just did! Even though many of us apply base 10 concepts to addition and subtraction without thinking, it is important we slow down and really understand what we are doing. Teaching the rules of our base 10 system and how to apply them is critical to helping learners correctly solve addition and subtraction problems
As the ABE Literacy Coordinator, I am working directly with students and tutors to establish this understanding of our base 10 system. During a meeting with a tutor/student, we use base 10 blocks, charts, and other materials to explore our numerical system and to apply it to math problems. If you would like to know more or have any questions, please call 814-238-1809. I would love to hear from you!
By: Amanda Giedroc, ABE Literacy Coordinator
References:
No last name, H. (2020), Place Value Chart: Thousands to Ones [Photograph], Math, Kids and Chaos. https://www.mathkidsandchaos.com/place-value-chart/
(N.d.), Interlocking Base Ten Blocks (Multi-Color, 121 Pieces), [Photograph], Rainbow Resource Center. https://www.rainbowresource.com/product/035105/Interlocking-Base-Ten-Blocks-Multi-Color,-121-Pieces.html?trackcode=googleBase



